MEASUREMENT: NOTES ON ANGLES

Like other fundamental mathematical concepts, 'angle' is a difficult idea, susceptible to a number of different interpretations. A good understanding of these interpretations is a long-term affair and children typically need a fair amount of relevant practical experience and discussion to develop a sound idea of what angle is.

Use of a protractor (especially the standard 180 degree protractor with clockwise and anti-clockwise scales) presupposes that the user has already formed some adequate notion of angle. Premature employment of the protractor may only obscure the central issue and lead to blind, mechanical use and a multitude of pupil errors.

The principles involved in the use of standard units apply equally to angular and linear measurement. The degree, which has its origins in Middle Eastern astronomy and does not relate well to our decimal system of numeration, is commonly accepted as the 'standard unit' of angular measurement. However, other systems could be effectively used, depending on the needs of the children - for example the number of 'part-turns' or complete 'revolutions' provide an obvious starting point for work in this area.

The simplest interpretation of 'angle' is as an 'amount of turn' and this can be made meaningful to young children by focusing their attention on a variety of situations, within their experience, involving things which turn, e.g. wheels, doors, hands on dials and, at the most personal level of all, the movement of their own bodies. The Valiant Turtle, controlled by commands RIGHT and LEFT, offers children a particularly vivid embodiment of this idea.

Though the Valiant Turtle is designed to turn in steps of one degree it is a simple task to write a program, in LOGO, so that the turtle will move through any required angle.

TO L
LT 90
END

TO R
RT 90
END

Once the basic idea of turning, clockwise and anti-clockwise, has been grasped, children will need a lot of practice estimating the amount of the turn. Achieving familiarity with measuring in degrees takes time for most children. The Valiant Turtle provides a good medium for these activities, giving instant feedback.

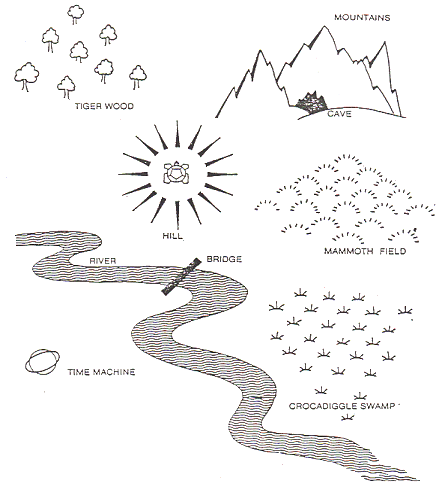
ACTIVITY 2: POINT YOUR TURTLE IN THE DIRECTION OF GRUB'S CAVE

A picture of the landscape could be presented to the children (FIG 5 shows one possible layout). The classroom landscape need only be a simple, makeshift one with arbitrary objects representing its features.

The turtle should be placed in the centre of the landscape and a child, who pretends to be Grub the caveman, stands next to it and points out the various landmarks to Myrtle. Other children instruct the turtle to face in that direction. Children should again be encouraged to estimate, or simply guess at first, and then try to improve upon their own and others' estimates.

It might be tempting to immediately introduce compass directions into such an activity. This would be inadvisable for young children since it could confuse the issue by combining two distinct ideas - a fixed frame of reference for directions, and the general notion of an angle as a turn relative to some arbitrary starting direction. For children with enough appropriate experience, combination of the two ideas might be feasible if they already have some experience of points of the compass and angles. In this case the opportunity might be taken to introduce the idea of bearings.

EXTENSION 2A: SPIN-AND-WIN

This is a game for up to 5 children. The turtle is placed in the centre of a circle 35 cm diameter and each player is issued with 10 paper counters as shown in FIG 6. One child operates the computer and the others are the players. The computer operator announces to the players the next turn instruction to be entered into the computer. Each player places one of their counters on the edge of the circle at the point they think the nose of their Valiant Turtle will be moved to by the instruction (more than one player can place their counter in a specific position). Only those who guess correctly keep their counter. Each child takes a turn to operate the computer and the winner is the child who loses the least number of counters.

Fig 6

Turns can be made left or right and one interesting suggestion the teacher can make to older children is turn the turtle through more than one revolution.

EXTENSION 2B: TURNING PUZZLES

Puzzle 1: What number do you use to turn the turtle, left or right, so that it comes back to where it started?

Puzzle 2: What number do you use to turn the turtle, left or right, so that it will face in the opposite direction?

Puzzle 3: What number do you use to get the turtle to turn through 2 complete revolutions?

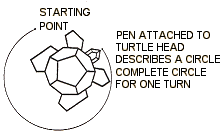
The children can find the answers to these and similar puzzles by trial and error. The results can be made visual by attaching a pen to the turtle's nose so that it can trace a line (see FIG 7).

Fig 7

Can the children understand the relationship between the number of turns and the numbers used to turn the turtle? (that is, 360 equals one turn, two turns equals 2x360 or 720 etc.).

FURTHER IDEAS:

1. Turn Turtle and Demolition Turtle, both in PENUP, are simple comparable activities that may be used here.
2. From the information given in the story, ask the children to draw their own illustrated map of the prehistoric landscape. Sorting out and co-ordinating the spatial relationships involved can be quite a demanding task for a group of young children. The resulting map can then be used as a guide to the construction of the landscape - on the floor.
3. If space and time allow, the landscape could be elaborated on and used as the focus of a whole topic, giving scope for model-building, art work and many kinds of creative writing.
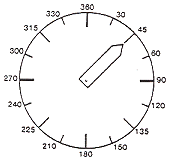
4. A simple aid to estimation of turns in degrees is a 'turtle compass' (FIG 8). This can be made quite simply from pieces of card or paper according to need.

Fig 8


5. For older children, compass directions can be incorporated into the scene and the turtle's movements related to them - further activities on using the turtle with the compass will be published in the Maps Microworld.

REFERENCES:

BELL. S.E. Rotation and Angles (Mathematics Longman 1967 in the Making Vol 4)

Many of the references cited in the previous sections are also pertinent here.