
|
Feedback Form

| Geometry Microworld for the Valiant Turtle |
POLYGONS: IRREGULAR POLYGONS
ACTIVITY 4: USE YOUR TURTLE TO MARK OUT THE EDGE OF A FIELD.
The children can pretend to mark out a field by 'direct driving' the turtle, starting and finishing at the same point. (N.B. It is not necessary at this introductory stage to insist that the turtle starts and finishes with the same orientation.) As the turtle travels around the edge of the field, blocks or counters could be used to mark the corners. The turtle's pen can, of course. be used to mark the field's perimeter on a large piece of paper.
EXTENSION 4A: THE TOTAL TURTLE TRIP THEOREM.
If the children record the movements made by the turtle they can use the results to become familiar with the 'Total Turtle Trip Theorem' (ref: Notes on Polygons - see above). This result can later be related to determining the angles in a polygon.
EXTENSION 4B: USE THE TURTLE TO MARK OUT MORE FIELDS.
FIG 19: See if the children can use the turtle to mark out two or three fields adjacent to each other - they need to solve a number of problems in order to 'fit' together some of the combined angles.
Fig 19
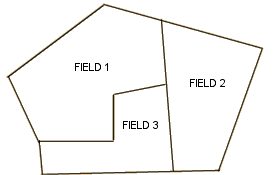
Another development of this idea is to include in the fields various objects representing property belonging to the individual farmers, e.g. a well, a house, a camel, etc.. Each field marked out has to include a particular farmer's property.
EXTENSION 4C: PATCHWORK.
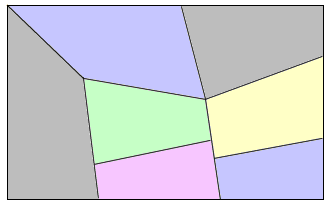
FIG 20: On a large sheet of paper have the turtle draw a patchwork pattern. A number of variations are possible, e.g. all shapes should have three sides, or four sides, or a mix of three and four sides, etc..
Fig 20
EXTENSION 4D: RACETRACK GAMES.
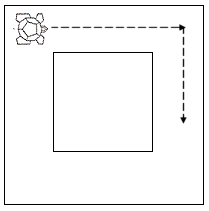
Although the 'Racetrack' game is introduced in PENUP, it is potentially such a rich activity that it warrants further treatment. A whole range of 'Racetrack' games can be played, either by individual children, or competitively. The goal could be the completion of one lap of a closed circuit in as few moves as possible (FIG 21).
Fig 21
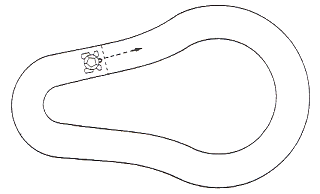
Again, trial-and-error is an almost inevitable strategy, especially on an irregular circuit, but strategies for achieving the 'fastest' lap can usefully be discussed.
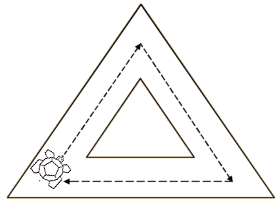
The development of more economical strategies may eventually be promoted by providing progressively more structured circuits (FIGS 22, 23 and 24). For example, the recognition that both the distances and the turns are about equal is a big step forward - even more the realisation that the whole process need only consist of a simple process repeated three times:
Fig 22
| Fig 23 | Fig 24 |
 |
 |
| e.g | FD 200 RT 90 FD 200 RT 90 FD 200 RT 90 FD 200 RT 90 |
or, once the REPEAT command has become familiar:
REPEAT 4 (FD 200 RT 90)
Note that little is likely to be achieved by forcing these ideas on the children. It is best suggested when the need becomes apparent.
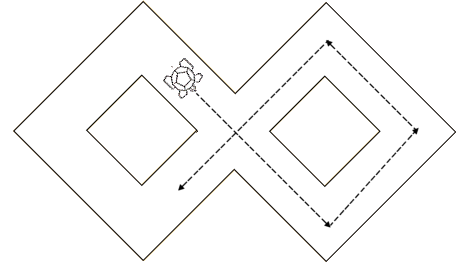
Another useful variation on this type of game is to design tracks with crossovers (see FIG 25).
Fig 25
EXTENSION 4E: WALKING TURTLE.
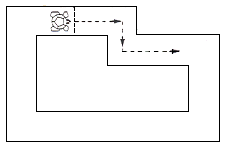
Take the turtle for a walk around part of the classroom but attempt to return it to its original position (and orientation, if possible) (FIG 26).
Fig 26
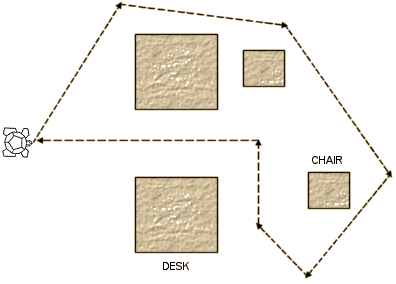
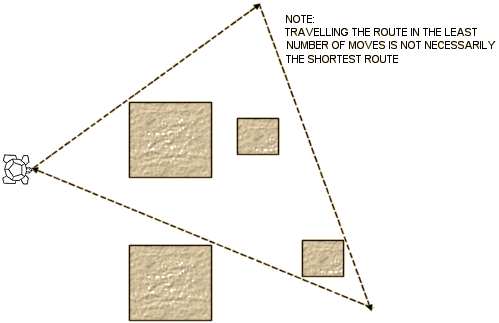
The walk can be constrained by requiring that the turtle should go round certain obstacles. Try to complete the walk in as few moves as possible.
EXTENSION 4F: HOW FAR DID MYRTLE TRAVEL AROUND THE FIELD.
By calculating the distance moved by the turtle around the field the children calculate the field's perimeter. It may be interesting to see how the children react to the problem of calculating the perimeter of fields with common boundaries.
This idea of calculating perimeter by examining the distance moved by the turtle can be preceded by the children being involved in activities suggested in Extension 3H. The development of the idea can of course be extended to all the other regular and irregular polygon activities. In particular the distance moved by the turtle can be used to judge success in the race track game.
FURTHER IDEAS.
- Get the children to mark out a 'field' themselves by 'playing turtle' (See 'b' below). A problem to be solved is that of specifying turns at all accurately!
- One practical approach for engaging children in activities 4 and 4B is to have them perform a drama using the storyline as a plot. Some of the children play the part of the farmers, someone the part of Ded-Loth, and someone else the part of Myrtle (this person is the computer operator). The farmers walk round their fields instructing Myrtle how to move. There is potential for dramatisation of some of the activities involving the Valiant Turtle. It has been all too commonly the case that the role of emotion and creative imagination in children's learning of mathematics has gone unrecognised.
- Find out more about the Ancient Egyptians and how they marked out their fields.
- (For older children). There is plenty of scope here for practical
geometry using quite 'primitive' instruments e.g. a non-stretch clothesline,
or length of thin rope, and some pegs.
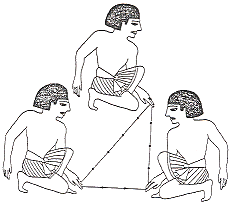
Mark off 12 equal segments on the line by tying knots at intervals (FIG 27). Apart from marking out lengths, the line can be used to mark out right angles when stretched out to form a 3-4-5 triangle (FIG 28).
Fig 27
Fig 28
Some related investigations are:
- Why is a right angle so special? Why is it so commonly used?
- Do any other triples of numbers give right angles?
- What other angles can be marked out in this way? Try a 4-4-4 triangle.
Try finding an answer to the above problems by experimenting with the turtle. Check the predicted results using the rope method.
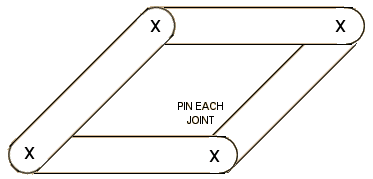
- Closed paths (polygons) can be investigated by quite young children
using plastic geostrips and paper fasteners (FIG 29). If these are not
available, strips of thick card of varying lengths, punched at either
end. can be used instead. A lot of free experimentation may be needed
in the early stages. Later, more specific problems and investigations
may be generated by restricting the number and/or the lengths of the
strips to be used.
Fig 29

- Using only strips of the same length, what shapes can be made?
- Use only 2 of one length and 2 of another (Fig 30).
- What different shapes can be made with only 3 strips (of any length)?
- Most of the figures made can be deformed to produce whole families of shapes. Which of the shapes are rigid?
- How can you make your other shapes rigid using as few extra strips as possible?
- (For older children). For each of the linkages of strips made, what is the greatest area it can contain.
Fig 30
REFERENCES:
GLENN, J.A. (Ed.) Children Learning Geometry. Harper and Row. 1979
| Back to index | Next page |
|---|