TURTLE GEOMETRY MICROWORLD 1

Exploring space with the floor Turtle brings a reality that cannot be obtained with a screen Turtle. The ideas of perimeter and, in particular, area, are difficult and abstract notions for the young mind to grasp. By moving through 'real' space, the floor Turtle can help to make the ideas become concrete and visible. Chris Gregory, Senior Lecturer in Mathematics at Bradford and Ilkley Community College, looks at the Geometry Microworld 1.

Perimeter
A number of activities in Adventures of Myrtle the Turtle explore the idea of the distance covered by a Turtle during its travels. When the journey starts and finishes at the same point, this distance represents the perimeter of the encompassed space. This can be determined by examining the program used to move the Turtle. It is important that children can distinguish between the numbers used for distance and those used for turning.

Perimeter of a Triangle and a Square

• Program the Turtle to draw triangles and squares of different sizes.
• Discuss the idea of perimeter.
• Place drawing pins at the corners of each shape.
• Wrap string around the pins without stretching it.
• Cut the string and lay it out.
• Ask the children to investigate the relationship between the length of the string and the numbers in their programs.
• Can they discover relationships between triangles of different sizes, squares of different sizes and the connection between the perimeters of squares and triangles?

Using procedures for creating the triangles and squares can help explain the relationships.

Area
The space encompassed by the Turtle represents the area of a shape. This is 'real' area and shape and, as such, is an effective teaching aid. Yet area is still a difficult concept for children to grasp because information about it cannot be extracted directly from looking at the numbers in the program. Nevertheless, there is a strong link between the Turtle activities and area activities already familiar in the classroom.

Investigating the area of a square
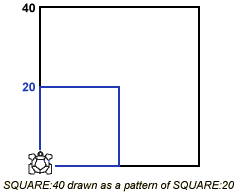
Program the Turtle to draw a square using the procedure SQUARE:20. Now ask the children to program the Turtle to draw a square "twice the size".
The most common response to this results in a SQUARE:40. This is generally a surprise and provides an ideal opportunity to discuss topics such as 'What does twice as large mean?'.

The child can verify that SQUARE:40 is four times the size of SQUARE:10 either by:

• Drawing and cutting out a number of SQUARE:20s in coloured paper and laying them over SQUARE:40.
• Instructing the Turtle to draw a pattern using SQUARE:20.

Developments

• Ask the children to repeat the SQUARE problem using SQUARE:10 with SQUARE:20.
• Ask them to estimate the area of SQUARE:40 in terms of SQUARE:10.
• Can they grasp that the number used to express the area of a shape is dependent on the choice of the base unit(s)?
• Can they discover the various arithmetical rules involved?

Let them investigate and test their conclusions by trying with other squares, e.g. SQUARE:30, SQUARE:50, etc.

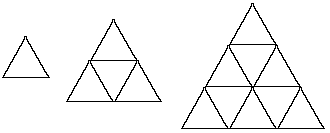
Area of similar shapes
The areas of different sizes of triangle can also be investigated.

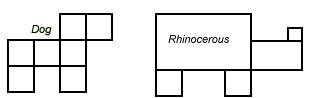Investigating the area of various shapes using the SQUARE procedure
Ask the children to build up shapes using the SQUARE:10 program. Ask them to comment on the areas of the shapes. Can they also estimate the area of shapes created from different sized squares?

Turtle drawing on squared paper
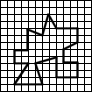Programming the Turtle to draw on squared paper can provide the opportunity for investigation not only of shapes made up from squares but also of other regular and irregular polygons. This can lead on to exploring the relationship between the area and perimeter of various shapes.

Investigating the relationship between area and perimeter
Ask the children if they can draw shapes with the same perimeter but different areas.

Cut outs
Another way of investigating the area of regular and irregular polygons is to program the Turtle to draw the shapes (in different colours) on plain paper. These can be cut out and the children asked which has the largest area. The smaller shapes can be cut up and made to cover the larger shape.

For older children
One extension to this investigation, suitable for older children using a screen Turtle, is to explore fractal geometry, where the perimeter approaches an infinite value while the area approaches a finite value.