TURTLE TESSELATIONS

In this article Chris Gregory, Senior Lecturer in Mathematics at Bradford and Ilkley Community College, looks at the way that the programming of basic shapes can be built upon.

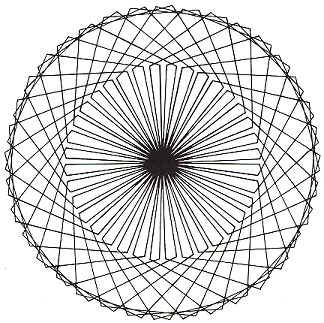
• Kaleidoscope patterns:
A classic Turtle graphics activity takes the form of producing patterns with a high degree of rotational symmetry by 'spinning' a polygon. Very attractive and complex patterns can be produced with very little effort.
e.g.

Some children have, in fact, invented similar procedures themselves.

Otherwise, it can be productive to give them this procedure and invite them to find out how it works and modify it to suit their own tastes. They could vary the polygon on which it is based and also the number of 'steps' in the pattern.

• Tessellations:
Regular hexagons can be fitted together edge-to-edge, without overlapping or leaving gaps, to make a pattern which can be extended indefinitely - a tessellation.

Time spent constructing and investigating tessellations can be very worthwhile. This is an excellent medium for exploring the properties of shapes, and the ubiquity of such patterns in the natural and man-made worlds ensures that this is a very useful stimulus for a variety of cross-curricular activities.

• Activity:
Using the procedure HEX, make the Turtle cover a large sheet of paper with hexagons. This is quite a challenging activity and very satisfying when some success is achieved.

A more modest project is to produce a limited pattern such as:

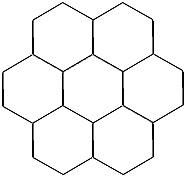
When all the necessary moves have been determined, try to put them all together into a superprocedure with a name such as HEXPAT.

It will help greatly if children have first hand experience of building up tessellations by physically fitting shapes together. The Mathematical Activity Tiles - MATS - are a cheap and attractive material for this purpose.

• Some further activities:
Try producing tessellations with other regular polygons (the gaps left between shapes can be just as interesting).
Here is a tessellation of squares:

Write a procedure which will draw it with the least possible number of straight lines.
Can the Turtle draw this without going over any line twice?

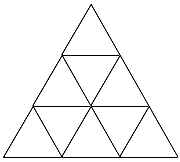
Do the same with this pattern of equilateral triangles.

Note: MATs are available from the Association of Teachers of Mathematics, Shaftesbury St., Derby.