
|
Feedback Form

| Geometry Microworld for the Valiant Turtle |
MEASUREMENT: LINEAR MEASUREMENT
ACTIVITY 1: USE YOUR TURTLE TO FIND THE WIDTH OF THE RIVER
FIG 1: Create an imaginary river on the classroom floor. Use chalk or two pieces of adhesive tape to mark the river banks. The children can use the turtle to discover the width of the river. They should be encouraged to estimate the input number required, and to try to improve on estimates already made.
Fig 1
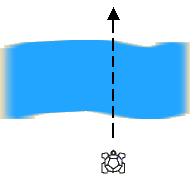
A lot of discussion of the practical issues involved may be necessary, especially with young children, and, for this reason, the activity might be best carried out by a small group. Issues to be resolved include - what do we mean by 'across' the river? How do we decide when the turtle has effectively crossed it? What is the minimum distance in 'turtle units' needed to cross the river?
Some children may only find it possible to arrive at a conclusion by trial and error, perhaps making a number of forward moves and eventually realising that the total distance is the sum of all the 'steps'. This strategy should not be discouraged but could be used as a focus for discussion by the whole group if necessary.
EXTENSION 1A: PLAYING WITH THE FORWARD COMMAND
Once the children have learned the first command (FORWARD) let them play with their new skill. Classroom results with this activity can be of great interest. Not only does it serve to illustrate the principles of LOGO teaching but can also vividly indicate the capability of the children.
An expected feature of this approach is for the children to invent their own activities. Measuring objects of their own choice is always more interesting to them. Even if the children simply move the Turtle forward they will begin to develop an appreciation of the relationship between the numbers they input into the computer and the distance moved by the Turtle.
Sometimes children start to question whether the Turtle can move backwards and turn. In one particular case they even discovered unaided the correct Primitive commands.
The excitement and interest generated by the children is the key to teaching the LOGO way. Thus when the children start to ask, "Can the Turtle turn?", it is an ideal time for the teacher to suggest the type of activity in the following section on Angles.
EXTENSION 1B: FIND THE WIDTH OF THE RIVER AT DIFFERENT POINTS
If, when the teacher creates the river she varies its width, the children can then be asked to measure it at different points.
EXTENSION 1C: MAKE A BRIDGE ACROSS THE RIVER
After the children have determined the width of the river, they could be asked to build a bridge across it. A good problem for discussion is "Where do we build the bridge?"
Some preparation is required for this activity. Pieces of card or paper; just wider than the turtle, should be joined together to form strips of differing lengths. Not all the strips should be long enough to span the river.
The children should use the turtle to determine the lengths of the various strips and then choose one suitable for building the bridge.
EXTENSION 1D: STEPPING STONE GAME
FIG 2: In this game several pieces of paper, 30 cm or larger in diameter, are placed at equal or irregular distances, to form a line of 'stepping stones' across the river.
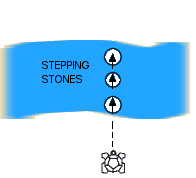
The children take it in turns to move the turtle from stone to stone across the river. They must always land precisely on one of the stones to avoid falling into the river and forfeiting their turn.
The children could play the target game, (see activity extension 1E below), as a prelude to this activity.
EXTENSION 1E: TARGET GAME
FIG 3: Place a sheet of paper on the floor. This is the 'target area' and should be large enough to accommodate the turtle. (Note: If the initial target is made very large the game can be made more difficult by gradually reducing its size until it is only just big enough to hold the turtle). Cut out a paper 'starting disc', 30 cm diameter, and position it some distance from the target area. The turtle is now placed on the disc facing in the direction of the target.
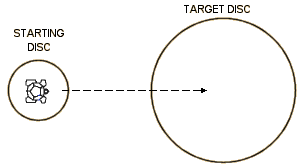
The children can make, and compare, predictions as to the number of FORWARD steps needed to make the turtle come to rest within the target area. These predictions can then be checked by driving the turtle forward.
This activity can, if desired, be used as the basis of a competitive game. The starting disc can be moved to positions at different distances from the target area and the game repeated.
EXTENSION 1F: HOW LONG AM I?
Get one of the children to lie down on a large piece of paper. One of the other children can draw around her outline. As in the previous activities the children can estimate the length of the outline in 'turtle units' and check the results using the turtle.
Finally the outlines can be cut out and labelled with the children's names and lengths and used as the basis of a classroom display.
A practical problem that inevitably arises is that of determining precisely where the journey should begin and end. One simple solution is to use the tip of the Valiant Turtle's nose. Alternatively the command PENDOWN could be used so that the length could be described quite explicitly and permanently by a straight line.
EXTENSION 1G: MYRTLE, THE FROG AND THE KANGAROO
When Myrtle was near the river Mr. Frog jumped in front of her and croaked, "I am Frog, the greatest long-jumper in the world". Now it so happened that Myrtle was with her good friend Kangaroo who was also very good at jumping. So they decided to have a competition. Myrtle was to be the judge.
Frog sat on a starting disc and took a mighty leap. He landed with a loud thud. "Bet you can't beat that", he grinned. "That would be easy", said Kangaroo, "I bet I could hop twice that far on one leg". Kangaroo did just that and Frog went home feeling very depressed.
Place the starting disc on the floor and ask the children to move the turtle forward to represent the Frog's jump. Return the turtle to the starting disc and ask the children to send the turtle to where Kangaroo landed.
Even if the children are too young to formally discuss scale in connection with this activity they can gain some practical experience of it.
In the preceding activities measurements were made using some agreed unit, whether 'turtle units' or centimetres etc.. In this activity. the 'unit' used is quite arbitrary. A comparison is made between two lengths, with one being taken as the unit of measurement and the other expressed in terms of the ratio of the two. In this activity the kangaroo jumped twice the distance of the frog. Scale is conventionally expressed as a ratio, 1:25. 1:100 etc..
Ask the children to imagine that other animals are involved in the competition. How far do they think each would jump compared with Frog? Use the turtle to measure the distance and mark the position where each animal landed. What about animals which cannot jump as far as Frog?
The turtle could also be used to measure how far the children themselves can jump.
FURTHER IDEAS:
a) At this point the game of Shove Turtle (presented in Valiant's documentation
- PENUP) is another way to practise estimating and determining distances.
b) FIG 4: A great deal of early work on the measurement of length can focus on the use of children's own 'personal units'. The analogy can be drawn between these units and the turtle's 'personal' unit.
Fig 4
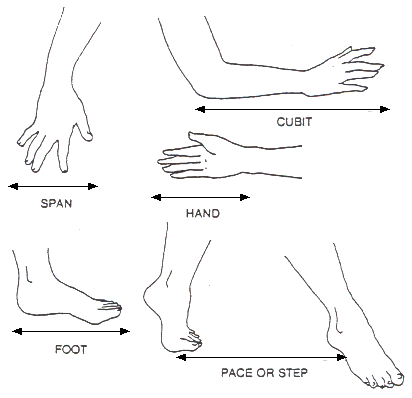
Children can use these units to measure a variety of distances and objects and compare the results with each other and with those obtained using the turtle.
c) The children's outlines, produced in activity extension 1F, could be measured in 'hands' and the results compared with those obtained in 'turtle units'. This may offer the children a means of making better estimates of the input numbers needed to drive the turtle a given distance.
d) Similar activities to the latter can be undertaken with any convenient, arbitrary units e.g. books, matchboxes, sticks etc..
e) With older children, relationships between such units can be explored systematically.
f) The historical use of personal units can be investigated, using reference books.
g) Some children may be interested in finding out about units of measurement of historical importance and their uses e.g. furlongs, poles, chains etc., or indeed units of measurement used in other cultures.
REFERENCES:
A great deal of valuable and relevant information can be found in reference books on the history of measurement, although some of the best books are out of print and obtainable only from libraries.
| See especially: | ||
| BOWMAN, M. | Romance in Arithmetic | Hutchinson 1964 |
| HOGBEN, L. | Man Must Measure | Rathbone 1955 |
| Older children will find a mine of useful information in: | ||
| DIAGRAM GROUP | The Book of Comparisons | Penguin 1980 |
| The Guinness Book of Records | ||
| Back to index | Next page |
|---|