POLYGONS: NOTES ON POLYGONS

The geometrical experience offered to Primary school children should include both two- and three-dimensional shapes. Conventional wisdom dictates that the earliest experiences should be with three-dimensional objects since these are 'real' and can be manipulated. Two-dimensional shapes, on the other hand, can be represented by drawings, rubber bands on pinboards, or by pieces of card or plastic but are nevertheless more 'abstract'.

When using the Valiant Turtle a natural starting point is two-dimensional shapes - in particular polygons (shapes with straight sides) - since the turtle can move only in straight lines. The emphasis in this situation is on polygons not as 'pieces' or 'areas' but as 'trails' or 'paths' traced out by the turtle. Since the children can readily relate to the turtle's movements, the shapes produced may be perceived by them as 'real' and 'concrete'.

The trails traced by the turtle in section 3 are 'open paths' - the turtle starts and finishes its journey in different locations and possibly with different orientations. In basic work with polygons the turtle completes a 'closed path', starting and finishing at the same point and with the same orientation.

Although easy to pose, the problem of making the turtle draw a closed path is very difficult without calling upon mathematical knowledge far beyond the reach of children at this stage. The strategy likely to be employed is trial and error. When the children's attention is later focused on regular polygons other, more systematic, approaches come within their reach.

A major difficulty encountered along the way may be a tendency to confuse the external angle (the amount of 'turtle turn', FIG 17) with the internal angle of the polygon. Here, encouraging the children to 'play turtle' and think about how much they actually turn themselves may help to clarify the situation.

Fig 17

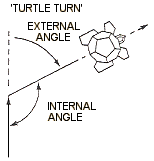
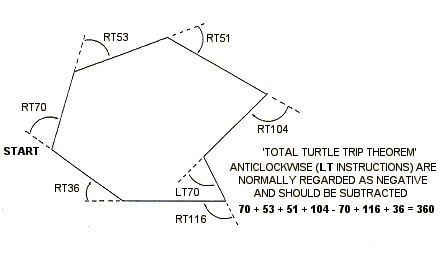
A basic result of this kind of activity, which children may eventually derive is what was termed by Papert and his colleagues the 'Total Turtle Trip Theorem'. This states that, if the turtle 'goes for a walk' and ends up in the starting position and pointing in the original direction, then it must have turned through some multiple of 360 degrees altogether. The total turn will be exactly 360 degrees in the case of a simple closed path with no crossovers (FIG 18). If children are ever to achieve a realisation of this, they will need to be encouraged to keep some record of their moves and engage in a great deal of discussion along the way.

Fig 18